Základnou jednotkou informácie je 1Bit [1 b] (binary digit). Je to najmenšia jednotka informácie. Môže nadobúdať dve hodnoty a to 1 alebo 0. Na popísanie viac ako dvoch stavov, je potrebné použiť viacero bitov. Počet potrebných bitov L matematicky určíme ako logaritmus počtu možností N pri základe 2.  L = log₂N.

Digitalizácia

Pri procese digitalizácie sa analógová informácia (alebo údaj) prevádza na digitálnu. Ku každému údaju sa priradí určitý počet bitov čiže jedinečná kombinácia jednotiek a núl. Toto priradenie musí byť také, aby sa údaj z digitálnej podoby dal jednoznačne pretransformovať späť do analógového tvaru.

Údaje digitalizujeme z dôvodu viacerých aspektov.

Hlavné aspekty digitalizácie:               -Spracovanie v PC
                                                              -Zmenšenie nárokov na objem prenesených dát

Podľa spôsobu získavania dát delíme digitalizáciu na:

primárnu digitalizáciu (je to napríklad získanie digitálneho obrazu priamym zberom digitálnou kamerou, prípadne iným snímačom.)

sekundárnu digitalizáciu (je to napríklad získanie digitálneho obrazu digitalizovaním analógového obrazu (snímky, mapy) spravidla skenerom.)

Digitalizácia údajov je nevyhnutným krokom k zjednodušeniu ľudskej práce, práve preto, lebo počítače ktoré nám uľahčujú prácu sú schopné spracovať iba zdigitalizované údaje.

Šifra

Šifrovanie používame na ochranu osobných údajov, čiže na zamedzenie prístupu k informácii osobe nato nepovolanej.

Šifrovanie delíme na symetrické a nesymetrické.

            -Symetrické šifrovanie zakóduje informáciu I podľa daného kľúča K a dostaneme zakódovanú správu S. Pokiaľ chceme správu S spätne dekódovať musíme poznať kľúč K použitý pri kódovaní správy. Tu nastáva problém s prenosom kľúča. Kľúč sa totiž musí preniesť na nejakom médiu medzi odosielateľom  a príjemcom správy. Toto môže byť nebezpečné z dôvodu odpočúvania pri prenose cez elektronický kanál, fyzický prenos je zase zdĺhavý. Tieto problémy rieši nesymetrické šifrovanie.

            -Nesymetrické šifrovanie zakóduje informáciu I podľa kľúča K1(často nazývaný verejný kľúč- public key) ktorý odosielateľ získa od príjemcu správy. U príjemcu je správa spätne dekódovaná pomocou kľúča K2(súkromný kľúč- private key) ku ktorému má prístup iba príjemca správy. To znamená, že zakódovanú správu odosielateľ po zakódovaní nedokáže spätne dekódovať, pretože nevlastní kľúč K2, ktorý je potrebný na dekódovanie. Verejný a súkromný kľúč sú jedinečné /k jednému verejnému existuje iba jeden súkromný/ a jeden z druhého sa nedajú nijakým spôsobom určiť.

      Dnes je šifrovanie zabezpečené na nesymetrickej úrovni už samotnými poštovými klientmi ako sú napríklad Mozilla Thunderbird, či Outlook (pozn. správa je šifrovaná symetricky, nesymetricky je šifrovaný iba šifrovací kľúč správy – dôvodom je časová náročnosť asymetrického šifrovania) . Šifrovanie dát pri komunikácii na webe zabezpečuje napríklad protokol HTTPS (čo je šifrovaný HTTP) alebo protokol SSH. Takéto šifrovanie sa používa najmä pri poskytovaní osobných údajov (kódy PIN, čísla účtov...) vzdialeným serverom.

Šifrovaním ale nerozumieme iba problematiku utajovania obsahu prenesených dát, ale aj integritu dát. To znamená, že pojem šifrovanie neobsahuje len ochranu údajov pred nepovolanými osobami, ale aj ich ochranu pred poškodením alebo úmyselným pozmenením dát. Toto zisťovanie chybovosti nazývame jednosmernou alebo hašovacou funkciou. Tieto funkcie sú neodlúčiteľnou časťou ochrany osobných údajov ako napríklad hesiel. Princíp je jednoduchý. Používateľ zadá svoje heslo pomocou hašovacej funkcie sa vytvorí jeho message digest (výstup z hašovacej funkcie) to s týmto message digestom sa bude neskôr porovnávať každé vloženie hesla. Výhodou tohto kódovania je to, že naše zadané heslo nefiguruje na serveri, namiesto neho je tam message digest, ktorý sa spätne nedá dešifrovať. Overenie užívateľa prebieha rovnako... zadané heslo sa pomocou hašovacej funkcie premení na message digest a ten sa následne porovnáva s message digestom uloženým v systéme. Ak sa zhodujú užívateľ je autentifikovaný a je vpustený do systému. Hašovacia funkcia je jednosmerná, takže stráca údaje, ide tu len o overenie či došlo k zhode message digestov (V modených operačných systémoch sa na hašovanie používa hašovacia funkcia MD5 alebo SHA-1).

Kódovanie

Kódovanie je proces, pri ktorom sa každému znaku alebo postupnosti znakov daného súboru znakov (vzorov) jednoznačne priradí znak alebo postupnosť znakov (obrazov) z iného súboru znakov.

Kódovanie je teda transformácia určitej informácie z jednej formy na druhú pomocou určitého postupu - algoritmu, ktorý je väčšinou verejne známy. Vo väčšine prípadov teda účelom kódovania nie je utajenie informácie (na rozdiel od šifrovania) ale len jej iná forma zápisu vybrané tak, aby sa informácia dala čo najlepšie alebo najúspornejšie uchovať alebo preniesť.

Vďaka počítačom sa najčastejšie sa používa kódovanie údajov a informácií do číselnej podoby. Takémuto kódovaniu tiež hovoríme Digitalizácia. Používa sa však aj nečíselné kódovanie.

Najčastejším problémom, pre ktorý sa neustále hľadajú nové riešenia je nájdenie nových úspornejších spôsobov kódovania pre čísla, znaky, text, zvuk, grafiku a video. Najčastejšie spôsoby kódovania jednotlivých údajov, pre ktoré sú v počítači definované určité operácie (sčítanie, násobenie, spájanie…), sú v počítači reprezentované dátovými typmi.

Kódovanie čísel v počítači

Všetky údaje v počítači sú kódované pomocou rôznej kombinácie hodnôt bitov [b] - najmenšej jednotky informácie. Každý z bitov môže nadobúdať iba dve rôzne hodnoty 0 a 1. Tieto bity sú však do pamäťových buniek počítača ukladané po osem, preto je výhodné na zakódovanie údajov použiť vždy taký počet bitov, ktorý je deliteľný ôsmimi (8,16,24,32 ....). Čím väčší počet bitov použijeme, tým väčší rozsah čísel môžeme použiť. Napríklad pomocou 8 bitov dostaneme 2⁸ = 256 rôznych kombinácií núl a jednotiek. Pomocou 8 bitov teda môžeme zakódovať napríklad čísla od 0 do 255 alebo čísla od -128 do 127 v prípade, že potrebujeme i záporné čísla. Na kódovanie čísiel v počítačoch je najvýhodnejšie použiť jedno „slovo“ (Word), t.j. taký počet bitov, ktoré počítač dokáže spracovať počas jednej operácie (jedného taktu procesora). Najmodernejšie počítače dnes používajú 64 bitové slovo, teda dokážu spracovať 64 bitov pri jednej operácií.

Kódovanie prirodzených čísel a nuly

Obrovskou výhodou je fakt, že každé číslo môžeme previesť do dvojkovej sústavy, ktorá používa iba cifry 0 a 1, čím pre každé číslo dostaneme jednoznačný zápis. Prirodzené čísla sú teda v počítači uložené v tzv. priamom kóde, čo je vlastne číslo prevedené do dvojkovej sústavy.

Pri použití jedného Bajtu (8 bitov) môžeme zakódovať 256 možných hodnôt, t.j. hodnoty 0 až 255 Pri použití 2 Bajtov (16 bitov) hodnoty 0 až 65535 Pri použití 4 Bajtov (32 bitov) hodnoty 0 až 4 294 967 295 Pri použití 1 slova moderného počítača (64 bitov) hodnoty 0 až

18 446 744 073 709 551 615.

         V niektorých prípadoch (napríklad pri prenose) je vhodnejšie použiť iný kód ako je zápis čísla v dvojkovej sústave. Jedným z takýchto kódov je kód BCD.

Kód BCD (Binary Coded Decimal) je jedným z najčastejšie používaných kódov na reprezentovanie desiatkových čísel. Pri tomto kóde je každá desiatková číslica zakódovaná pomocou štyroch bitov.

Tento kód kvôli rôznym výhodám či nevýhodám bol rôzne modifikovaný. Boli pozmenené váhové stavy jednotlivých bitov kódu, preto sa začali tieto váhy dopisovať za označenie kódu BCD. Klasickému kódu prislúcha kód 8421, kde prvý bit s prava má váhu čísla 1, druhý váhu čísla 2, tretí váhu čísla 4 a posledný váhu čísla 8. Napríklad číslo BCD 8421 kóde 0111 predstavuje číslicu 7 (8.0 + 4.1 + 2.1 + 1.1). Známe sú tiež kódy BCD 2421, BCD 84-2-1 alebo kód BCD 8421 firmy IBM, ktorý nulu kódoval bitmi 1010.

Kódovanie celých čísel

Pri celých číslach je potrebné zohľadniť i znamienko. Pretože sú znamienka len dve (+, -), môžeme ich zakódovať pomocou jedného bitu (0 = +, 1= -). Pri kódovaní celých čísel sa znamienko zakóduje vždy prvým bitom zľava. Napr. pri použití 1 Bajtu bude 10011101 kód pre -29.

-Pri použití 1 Bajtu (8 bitov - 1 bit znamienko a 7 bitov hodnota), môžeme zakódovať hodnoty -128 až +127

-Pri použití 2 Bajtov (16 bitov -1 bit znamienko a 15 bitov hodnota), môžeme zakódovať hodnoty -32 768 až +32 767

-Pri použití 4 Bajtov (32 bitov - 1 bit znamienko a 31 bitov hodnota), môžeme zakódovať hodnoty -2 147 483 648 až +2 147 483 647

-Pri použití 4 Bajtov (64 bitov - 1 bit znamienko a 63 bitov hodnota), môžeme zakódovať hodnoty -9 223 372 036 854 775 808 až +9 223 372 036 854 775 807

Kódovanie reálnych čísel

Reálne čísla môžeme do počítača kódovať dvoma spôsobmi:

Ako čísla s pevnou rádovou čiarkou (tento spôsob sa väčšinou používa na uloženie meny napr.: 24,50 Sk). Pri tomto spôsobe je niekoľko bitov vyhradených pre celú časť čísla a niekoľko pre desatinnú časť čísla. Ak nám pri nejakej operácii dostaneme väčší počet desatinných miest ako môžeme zakódovať pomocou vyhradeného počtu bitov, vtedy sa zvyšné miesta jednoducho odrežú a nebudú do pamäte počítača uložené.

Ako čísla s pohyblivou rádovou čiarkou – tu je vyhradených niekoľko bitov pre hodnotu čísla (mantisu) a zvyšok je vyhradený pre exponent. Napr.: číslo 126,567 je uložené ako 126567.10-3. V našom prípade je mantisa 126567 a exponent -3. Obe tieto hodnoty sú uložené samozrejme v priamom kóde a majú 1 bit vyhradený pre znamienko.

Kódovanie znakov

Na rozdiel od čísel, znaky textu nevieme previesť do dvojkovej sústavy, preto bolo potrebné vymyslieť iný spôsob ako jednoznačne priradiť určitému znaku práve jednu kombináciu núl a jednotiek, ktorá tento znak v počítači bude reprezentovať. Keďže neexistuje žiadny univerzálny spôsob ako to urobiť, každý výrobca počítačov tento problém riešil iným spôsobom, preto existuje viacero znakových kódov. Poriadok do tohto chaosu sa snažil zaviesť americký úrad pre normalizáciu, ktorý vyhlásil jeden spôsob, ktorý by mali všetci používať. Tento spôsob kódovania sa volá ASCII - American Standard Code for Information Interchange (Americký štandardný kód pre výmenu informácií).

Tento štandard hovorí, že na zakódovanie každého znaku sa použije 8 bitov. Čo umožňuje definovať kód pre 256 znakov. Pričom prvá polovica znakov bude pre všetky krajiny rovnaká a zvyšných 128 znakov sa pre každú krajinu stanovil podľa ich potrieb. Tento spôsob vniesol do kódovania znakov neuveriteľný chaos, preto sa vymyslel nový spôsob kódovania UNICODE.

UNICODE - je medzinárodný štandard, ktorého cieľom je definovať jedinečný kód zvaný code point pre každú z grafém používaných na zápis ľudského jazyk. Vznik jednotného kódu znakov, podmienila existencia množstva znakových sád. Znakové sady sa líšili nielen pre jednotlivé krajiny, ale i v rámci jednej z krajín existovalo viacero znakových sád. Kódovanie UNICODE je navrhnuté pomocou dvojbajtového kódovania znakov, čo umožňuje vytvárať sady s 65 536 znakmi. Štandard je navrhnutý tak, že všetky možné znaky rozdeľuje do sedemnástich dvojbajtových plánov. Takéto rozdelenie umožňuje definovať až 1 114 112 (= 17 × 216) znakov. Prvá verzia štandardu vznikla v októbri 1991 no súčasná verzia štandardu je už UNICODE 5.0. Táto definuje 101 063 znakov čo je iba 9,1 % zo všetkých možných.

Kódovanie farieb

 Aby bol obrázok farebný, musíme každému bodu - pixelu obrázka priradiť určitú farbu. Spôsobov, akými sa to dá urobiť je opäť niekoľko. Na to, aby sme to vedeli urobiť, musíme vedieť niečo o ľudskom oku a spôsobe videnia farieb. Farby vnímame vďaka svetlu, ktoré vstupuje do nášho oka a dopadá na bunky - čapíky, ktoré sú citlivé na farbu. Svetlo je vlastne elektromagnetické vlnenie s rôznou vlnovou dĺžkou. Ľudské oko dokáže vnímať iba určitý rozsah vlnových dĺžok svetla. Svetlo s najväčšou vlnovou dĺžkou, ktoré ľudské oko vníma, je červenej farby (780 nm) a svetlo s najnižšou vlnovou dĺžkou je svetlo fialovej farby (380nm). V tomto spektre farieb je ľudské oko schopné bez problémov rozlíšiť vyše 1,5 milióna rôznych farieb. Nie však každej farbe, ktorú rozlíšime pripadá iná vlnová dĺžka, pretože podľa intenzity dopadajúceho svetla, ľudské oko rozlišuje sýtosť a jas daného odtieňa farby. Takže iná vlnová dĺžka prislúcha iba rôznym odtieňom farieb.

Farebné modely HSB a HLS

Prvé riešenie problému kódovania farieb, ktoré sa ponúka, je zobrať celý rozsah vlnových dĺžok a rozdeliť ho na niekoľko častí a do pamäte počítača uložiť poradové číslo farby, ktorej prislúcha určitá vlnová dĺžka, ďalej jej sýtosť a jas. Kódovanie farieb takýmto spôsobom využívajú farebné modely HSB (či HSV), HLS Oba modely uchovávajú informáciu o. odtieni (Hue) a sýtosti (Saturation). Odlišujú sa iba v tom, že prvý model používa jas (Brightness) a druhý používa svetlosť (Lightness). V prvom modeli dostaneme čiernu farbu tým, že nastavíme jas na nulu a bielu tak, že jas nastavíme na maximálnu hodnotu (nezávisle od sýtosti). V druhom modeli dosiahneme čiernu, ak je svetlosť aj sýtosť 0 a bielu, ak je svetlosť aj sýtosť maximálna. Hlavným nedostatkom tohto problému je náročnosť vyrobenia svetla so zadanou vlnovou dĺžkou. Naštastie existujú aj iné riešenia problému kódovania farieb.

Farebný model RGB

Farebný model RGB je najčastejšie využívané kódovanie farby bodu obrázka. Empiricky sa zistilo, že takmer všetky farby sa dajú vytvoriť zmiešaním ľubovoľných troch nezávislých farieb (t.j. že pomocou zmiešania dvoch nedostaneme tretiu). Najvýhodnejšie pre výrobu svetelných lúčov (aditívny farebný systém) bolo použitie farieb červená (Red), zelená (Green), modrá (Blue). Aby sme vedeli vytvoriť 1,5 milióna farieb stačí, ak každú z týchto farieb rozdelíme na 115 oddtieňov, ktorých zmiešaním v rôznych pomeroch vzniknú všetky farby. Kvôli uchovaniu v pamäti počítača, je však výhodnejšie použiť až 256 odtieňov každej farby (8 bitov), čo nám umožní vytvoriť až 16 777 216 rôznych farieb. Pri takomto kódovaní je každá farba zakódovaná 24 bitmi, čo sú tri pamäťové miesta počítača. Pričom 255 0 0 je sýta červená farba, 0 255 0 je sýta zelená farba, 0 0 255 je sýta modrá farba, 0 0 0 je čierna farba a 255 255 255 je biela farba.

Farebný model CMY

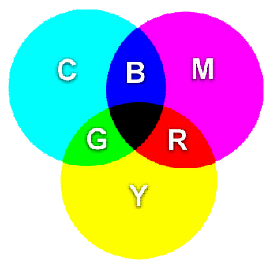Farebný model CMY je model, ktorý používa doplnkové farby (substraktívny farebný systém). V modeli RGB platilo, že ak zmiešame všetky tri základné farby s maximálnou sýtosťou, dostaneme bielu farbu. Takýto spôsob je výhodný pri obrazovkách monitorov, pretože tienidlo je čierne. Pri tlačiarňach sa však tlačí na biely papier, preto potrebujeme vziať také farby, pri ktorých, ak zmiešame ich najsýtejšie odtiene, dostaneme čiernu farbu. Takéto farby dostaneme, keď zoberieme doplnkové farby k farbám červená, zelená a modrá. Týmito farbami sú azúrová (Cyan), purpurová (Magenta) a žltá (Yellow). Kvôli tomu, že je lacnejšie vyrobiť čierny atrament ako ho miešať pomocou týchto troch farieb, sa k týmto farbám pridáva i samostatná čierna farba a tento model sa označuje tiež CMYK, kde posledné písmeno je odvodené od blacK - čierna . Výhodou tohto formátu je tá, že výsledná farba CMY sa dá veľmi jednoducho získať z modelu RGB pomocou vzorcov:
                                               C = (255 - R); M = (255 - G); Y = (255 - B)

Farebný model YUV

Farebný model YUV slúži na zachovanie čiernobielej informá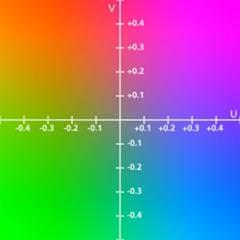cie pri televíznom vysielaní. Po vzniku farebného filmu nastal problém, ako zakódovať farbu tak, aby farebné filmy mohli pozerať i ľudia s čiernobielymi prijímačmi. Bolo potrebné zachovať pôvodnú čiernobielu informáciu a doplniť ju tak, aby vznikol farebný obraz. Farba je kódovaná tak, že k čiernobielej zložke Y, ktorú tiež nazývame svietivosť (luminance), pridáme dve farebné zložky UV farebnosti (chrominance), pričom zložka U udáva odtieň medzi modrou a žltou a zložka V udáva odtieň medzi červenou a žltou farbou. Takže čiernobiely prijímač berie do úvahy iba zložku Y, farebné prijímače za pomoci zložiek YUV získajú RGB kód farby pomocou jednoduchej transformácie:

R = Y + 1,403V; G = Y - 0,344U - 0,714V; B = Y + 1,770U

Číselné sústavy - prevody

Číselné sústavy môžeme rozdeliť do dvoch kategórií - pozičné a nepozičné. Medzi nepozičné sústavy patria napríklad rímske čísla. Pozičné číselné sústavy sú sústavy pozostávajúce z určitého počtu cifier (v desiatkovej ich je desať 0 - 9), ktoré sú usporiadané do pozícií, ktoré sa tiež nazývajú rády. Tá istá cifra umiestnená na inom ráde má inú hodnotu. Rády sú číslované sprava doľava od 0 vyššie, pretože prvá cifra sprava má najmenšiu hodnotu. V desiatkovej sústave posunutím cifry o jedno miesto (rád) doľava, cifra nadobudne desaťkrát väčšiu hodnotu. V dvojkovej sústave posunutím cifry o jeden rád doľava, cifra bude mať dvakrát väčšiu hodnotu.

Prevod čísel do desiatkovej sústavy.

Číslo v ľubovoľnej sústave sa do desiatkovej sústavy prevedie nasledovne:

1. Očíslujeme si rády čísla, t.j. pod prvú cifru sprava napíšeme 0 pod druhú 1 pod tretiu 2 ...
2. výsledné číslo v desiatkovej sústave potom dostaneme ako súčet cifier vynásobený základom sústavy na príslušný rád.

Tento postup funguje pre všetky sústavy vrátane desiatkovej (prevod do seba sama). Napríklad číslo 10294 sa dá popísaným postupom napísať takto:

10 294 = 3.10⁴ + 0.10³ + 2.10² + 9.10¹ + 4.10⁰

Číselnou sústavou používanou v počítači je dvojková - binárna sústava (kvôli jednotke informácie 1 bitu, ktorý môže nadobúdať dve hodnoty 0 a 1). V jednej pamäťovej bunke počítača je však 8 bitov, preto vždy doplňujeme cifry tak, aby bol ich počet deliteľný číslom 8 (8, 16, 24, 32 ...).

(01101100)_b = 0.2⁷ + 1.2⁶ + 1.2⁵+0.2⁴ + 1.2³ + 1.2² + 0.2¹ + 0.2⁰ =108

Pri sústavách so základom vyšším ako 10 (napríklad šestnástkovej) pre vyššie cifry nemáme prislúchajúce symboly, preto ich nahrádzame písmenami (v šestnástkovej sústave sú to písmená ABCDEF, kde A=10, B=11, C=12, D=13, E=14, F=15).

Obrovskou výhodou šestnástkovej - hexadecimálnej sústavy je to, že hodnotu, ktorú v dvojkovej sústave je potrebné zapísať pomocou 8 cifier, v šestnástkovej zapíšeme presne pomocou dvoch cifier. Napríklad najvyššia možná hodnota v dvojkovej sústave, ktorá sa dá zapísať pomocou 8 cifier, v šestnástkovej sústave zapíšeme (11111111)_b = (FF)_H. Príklad prevodu do desiatkovej sústavy:

(E4)_H = E.16¹ + 4.16⁰ = 14.16¹ + 4.16⁰ = 228

Prevod čísel z desiatkovej do inej sústavy.

Ak chceme previesť číslo z desiatkovej sústavy do inej sústavy, musíme číslo deliť základom sústavy, do ktorej číslo chceme previesť, až pokiaľ nedostaneme číslo nula. Po každom delení si zapíšeme zvyšok, pričom zvyšok po prvom delení je cifra najnižšieho (nultého) rádu, zvyšok po druhom delení udáva cifru prvého rádu ... Takto napríklad prevedieme číslo 215 do dvojkovej sústavy:

215 : 2 = 107; 107 : 2 = 53; 53 : 2 = 26; 26 : 2 = 13; 13 : 2 = 6; 6 : 2 = 3; 3 : 2 = 1; 1 : 2 = 0
zvyšok 1           zvyšok 1       zvyšok 1      zvyšok 0       zvyšok 1  zvyšok 0  zvyšok 1  zvyšok 1

Výsledok teda je 11010111 (zvyšky zapísané v opačnom poradí).

A takto rovnaké číslo 215 prevedieme do šestnástkovej sústavy.

215 : 16 = 13; 13 : 16 = 0;
zvyšok 7           zvyšok 13 (to zodpovedá symbolu D)

Výsledok je teda D7.

Rovnako funguje i prevod z desiatkovej sústavy do seba sama.

215 : 10 = 21; 21 : 10 = 2; 2 : 10 = 0;
zvyšok 5           zvyšok 1     zvyšok 2

Dostali sme teda skutočne číslo 215.

Prevod čísel z dvojkovej do šestnástkovej sústavy.

Sila šestnástkovej sústavy, ako som písal vyššie, spočíva v jednoduchšom zápise čísla z dvojkovej sústavy. Jednoduchší zápis by však bol na nič, keby bol prevod z dvojkovej sústavy do šestnástkovej zložitý. Našťastie je veľmi jednoduchý. Stačí číslo dvojkovej sústavy rozdeliť na štvorčíslia začínajúc od najnižšieho rádu (teda sprava). Každé štvorčíslie môže nadobúdať hodnoty od 0 do 15, čo je práve jedna cifra čísla šestnástkovej sústavy. Napríklad číslo 11010111 prevedieme nasledovným spôsobom:

11010111 = 1101 0111; (1101)_b = (13)_d =(D)_H; (0111)_b = (7)_d =(7)_H

Takže výsledok je D7.

Algoritmus

Algoritmus je konečná postupnosť definovaných inštrukcií na splnenie určitej úlohy.

Algoritmy môžu byť zapísané (implementované) vo forme počítačových programov. Logická chyba v algoritme môže viesť k zlyhaniu výsledného programu.

Pojem algoritmu sa často ilustruje na príklade návodu, hoci algoritmy sú často oveľa zložitejšie. V algoritmoch sa často niekoľko krokov viacnásobne opakuje (iterácia), alebo ďalší postup závisí od aktuálneho stavu (vetvenie).

Na riešenie tej istej úlohy môže existovať niekoľko rôznych algoritmov s rôznymi postupnosťami inštrukcií. Rôzne algoritmy sa tiež môžu líšiť v množstve času a pamäte potrebných na splnenie úlohy.

Vlastnosti algoritmov

Konečnosť

Každý algoritmus musí skončiť po vykonaní konečného počtu krokov. Tento počet krokov môže byť ľubovoľne veľký (podľa rozsahu a hodnôt vstupných údajov), ale pre každý jednotlivý vstup musí byť konečný. Postupy, ktoré túto podmienku nespĺňajú, sa môžu nazývať výpočtové metódy. Špeciálnym príkladom nekonečnej výpočtovej metódy je reaktívny proces, ktorý priebežne reaguje s okolitým prostredím.

Determinizmus

Každý krok algoritmu musí byť jednoznačne a presne definovaný; v každej situácii musí byť úplne zrejmé, čo a ako sa má vykonať, ako má vykonávanie algoritmu pokračovať. Pretože bežný jazyk zvyčajne neposkytuje úplnú presnosť a jednoznačnosť vyjadrovania, boli pre zápis algoritmov navrhnuté programovacie jazyky, v ktorých má každý príkaz jasne definovaný význam. Vyjadrenie algoritmu v programovacom jazyku sa nazýva program.

Vstup

Algoritmus zvyčajne pracuje s nejakými vstupmi, veličinami, ktoré sú mu odovzdané pred začatím jeho vykonávania, alebo v priebehu jeho činnosti. Vstupy majú definované množiny hodnôt, ktoré môžu nadobúdať.

Výstup

Algoritmus má aspoň jeden výstup, veličinu, ktorá je v požadovanom vzťahu k zadaným vstupom, a tým tvorí odpoveď na problém, ktorý algoritmus rieši.

Efektivita

Všeobecne požadujeme, aby algoritmus bol efektívny, v tom zmysle, že požadujeme, aby každá operácia požadovaná algoritmom, bola dostatočne jednoduchá na to, aby mohla byť aspoň v princípe prevedená v konečnom čase iba s použitím ceruzky a papiera.

Všeobecnosť

Algoritmus nerieši jeden konkrétny problém (napr. „ako vypočítať 3×7“), ale rieši všeobecnú triedu obdobných problémov (napr. „ako vypočítať súčin dvoch celých čísel“).

Komprimácia – kompresia

Komprimácia (kompresia, pakovanie či balenie) dát je proces, pri ktorom sa znižuje objem dát, pričom existujú dva druhy komprimácie:

·         nestratová - pri ktorej nedochádza k strate údajov. To znamená, že ak skomprimované dáta dekomprimujeme, získame úplne identické dáta. Takto sa balia napríklad textové, programové a iné súbory. Kompresia sa deje na základe vynechania redundantných (nadpočetných) informácií. Kompresný pomer, ktorý predstavuje pomer medzi veľkosťou dát pred spakovaním a po ňom, sa tu dá dosiahnuť až okolo 2:1, niekedy aj viac, to však závisí od druhu dát.
 

·         stratová - je proces, pri ktorom sa vynechajú tie údaje, ktoré sú pre celkový dojem z dát nepodstatné. Kompresný pomer je niekedy až 200:1, ale dáta sa už po kompresii nikdy nedajú zrekonštruovať do pôvodnej podoby. Časť informácií totiž chýba. Stratovú koprimácia používa hlavne pre komprimovanie mediálnych súborov a to zvuk, obraz, video ... Aj keď komprimačný pomer sa zdá veľmi veľký, aj pri niekoľko desaťnásobnej redukcii dát je výsledok komprimácie takmer nerozoznateľný od originálu. Platí to najmä pre obrázky vo formáte JPG, alebo video vo formáte MPEG. Cenou za to je veľmi zložitý postup komprimácie a nutnosť použiť zložité matematické metódy.
Z princípu stratovej komprimácie jednoznačne vyplýva, že nie je možné komprimovať touto metódou napríklad textový súbor. Po jeho dekompresii by sme nedostali čitateľné dáta. Obrázok by sa, naopak, dal skomprimovať pomocou nestratovej komprimácie, pričom by sme dosiahli komprimačný pomer obvyklý pre nestratovú komprimáciu. Táto metóda je výhodná vtedy, ak chceme znížiť ojem dát aspoň v menšom komprimačnom pomere, ale sa nechceme vzdať detailov, ktoré by sa pri stratovej komprimácii stratili.
Komprimácia sa používa najčastejšie na zníženie objemu multimediálnych dát pri prenose dát v sieťach (v internete).

·         Komprimácia sa vykonáva buď automaticky (uložením súboru v komprimovanom formáte JPG, MPEG, MP3) alebo pomocou špecialneho komprimačného programu (ZIP, RAR). Dekomprimácia sa deje buď samorozbalením alebo pomocou špeciálneho dekomprimačného programu. Niektoré dáta ostávajú trvale vo svojej komrimovanej podobe (najmä pri stratovej kompresii).

      Výhodou archivačných formátov ako sú WinRar, WinZip, 7Zip je, že dokážu do jedného balíka vložiť množstvo súborov čo je výhoda, ktorú určite oceníme napríklad pri mailovaní . Ak však archivujeme súbory len za účelom zníženia ich veľkosti je dobre si uvedomiť, že komprimovať sa oplatí len súbory, na ktorých ešte nie je aplikovaná žiadna kompresia. Aj preto majú napríklad obrázky vo formáte TIFF alebo BMP po pridaní do archívu veľmi malú veľkosť, zatiaľ čo obrázky v JPEG nezmenšíme takmer vôbec. To isté platí aj o hudobných súboroch. Veľmi efektívne je komprimovať textové dokumenty, databázy, súbory s poštou.